Die kapazitive dielektrischen RF-Erwärmung [i],[ii] (Radio Frequency Heating) koppelt die Energie eines elektrischen Wechselfeldes in das Material ein. Es eignen sich elektrisch gering bis nichtleitende Materialien wie die meisten Lebensmitteln vorliegt.
Die Erwärmung erfolgt "von innen heraus" durch die Interaktion des Materials mit einem kontaktlos angelegten elektrischen Wechselfeld. Im RF-Bereich dominiert die Energieeinkopplung in ionische Materialanteile wie Salze und polaren Gruppen. Normalerweise ungeordnete ionische Ladungsträger richten sich in einem elektrischen Wechselfeld (z.B. mit 13,56 Mio Schwingungen pro Sekunde) jeweils neu aus und erzeugen eine interne "Reibung", so das sich das Material von innen heraus erwärmt.
Für technische Zwecke sind 13,56, 27,12 und 40,68 Mhz (sog. ISM-Bänder) freigegeben und nutzbar.
Mit dem kontaktlosen Wirkprinzip können technische Wärmeübertragungsprobleme, bedingt durch eine zu geringe Wärmeleitfähigkeit des Materials in vorteilhafter Art und Weise gelöst werden. Zudem wird kein Wärmeübertrager oder ein Wärmetransportmedium benötigt, Überhitzungen an Wärmeübertrageroberflächen und hygienisch immer problematische Anbackungen entfallen somit. Wichtig ist, das nur das Gut erwärmt wird, nicht aber die technische Peripherie.
Im Vergleich zu den bekannten Mikrowellenerwärmungen arbeiten RF-Verfahren bei erheblich größere Wellenlängen und i.d.R. ausreichend hoher Leistungsdichte. Mikrowellensysteme (2,45GHz) koppeln elektromagnetische Energie ausschließlich durch Dipolpolarisation in den Wasseranteil ein. Bei einer Wellenlänge um 12,5 cm, d.h. für eine volle Periode, treten ca. alle 3cm Maxima und Minima auf, die bei einem ruhenden Gut als „stehendes“ Erwärmungsmuster bemerkbar sind.
RF-Erwärmungen nutzen physikalisch ähnliche Wirkmechanismen, jedoch bei viel niedrigeren Frequenzen. Dadurch treten signifikante Unterschiede auf.
-
die Wellenlänge mit 10…30m erheblich größer, so dass selbst größere Objekte von 1…2m Ausdehnung relativ zur Wellenlänge immer noch klein sind,
-
die Eindringtiefe in das Material ist drastisch höher als bei Mikrowellen- und Infraroterwärmungen, sie reicht in den Meter - Bereich,
-
es dominiert der ionische Einkopplungsmechanismus.
Die Dipol-Einkopplung in Wasser spielt eine untergeordnete Rolle, sie erreicht erst ab ca. 900MHz eine mit der ionischen Einkopplung vergleichbare Größenordnung. Die ionische Energieeinkopplung fällt im Ghz-Bereich massiv ab.
Im RF-Bereich wird in Wasser nahezu keine Energie eingekoppelt, sodass Feuchte- und Wärmeausgleichsprozesse im Material sehr wirksam erfolgen können. Meistens stellt die Feuchteabfuhr von der Oberfläche den limitieren Schritt dar.
Insgesamt ergeben sich deutlich andere Charakteristika, die es erlauben, Erwärmungen gleichmäßig zu realisieren, ferner ist die Neigung zu Hot-Spots [iii],[iv] (lokale Überhitzungen) deutlich geringer.
Das RF-Verfahren weist eine temperaturabhängige, nichtlineare Einkopplungsfunktion auf [v], die in der Ansteuerung zu berücksichtigen ist. In gut abgestimmte RF-Erwärmungen sind interne Temperaturdifferenzen im Material unterhalb weniger °C erzielbar.
Zusammen mit der hohen Eindringtiefe bietet sich das RF-Verfahren in Trocknungen hervorragend für die Beschleunigung der durchsatzlimitierenden letzten, langsamen Trocknungsphase an.
Die Technologie für RF-Erwärmungen wurde historisch mit in der Frequenz freilaufenden Röhrengeneratoren realisiert. Da die EMV-Anforderungen in den letzten Jahrzehnten drastisch angestiegen sind, wurden sie durch eine besser beherrschbare Festfrequenztechnik abgelöst. Moderne Halbleitersysteme arbeiten mit dem 50Ohm Standard.
Prinzipieller Aufbau eines HF-Erwärmungsystems:
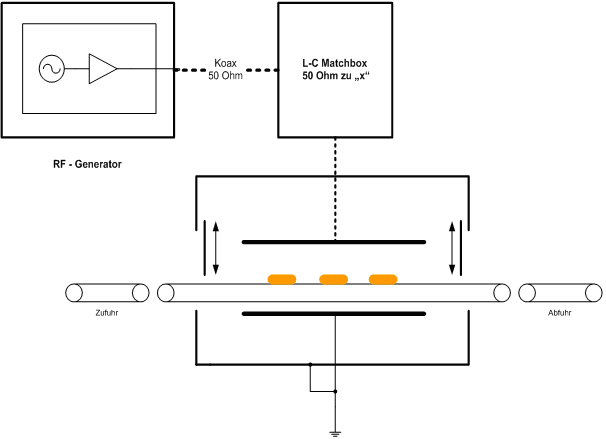
Einsatz- und Effizienzaspekte des Verfahrens
Die erforderliche Wärmeleistung lässt sich zwar über Masse und Wärmekapazität des Gutes und den Energieaufwand zur Wasserverdampfung recht einfach bestimmen. Die interessante Fragestellung lautet, welche RF-Leistung benötigt wird und mit welchen Stromverbrauch diese bereitgestellt werden kann. Da der abdeckbare Leistungsbereich bis zu einigen 10kW reichen kann, ist eine fallweise Prüfung erforderlich. Als erster Richtwert kann eine thermische Umsetzung von ca. 75% der eingesetzten HF-Leistung in Wärme gelten. Der elektrische Wirkungsgrad der RF-Erzeugung ist Fabrikatabhängig, derzeitige Systeme erreichen bis zu ca. 85%. Der tatsächliche Energiebedarf ist natürlich vom Grad der Wärmerückgewinnung des Prozesses abhängig. Aus Bäckereiapplikationen sind Energieeinsparungen von bis zu 30% gegenüber vergleichbaren konventionellen Lösungen bekannt.
Für den genauso relevanten Durchsatzaspekt kommt die verzögerungsfreie Wärmeerzeugung zum Tragen. Publizierte Umrüstungen von Backstraßen geben bei gleichen baulichen Abmessungen Durchsatzsteigerungen von bis zu 40% an
[v] Chan, C. T., Tang, J., Younce, F., 3-Dimensional Numerical Modeling of an Industrial Radio Frequency Heating System Using Finite Elemente, J. of Microwave Power and Electrom. Energy, Vol. 39, No. 2, (2004): 87-106